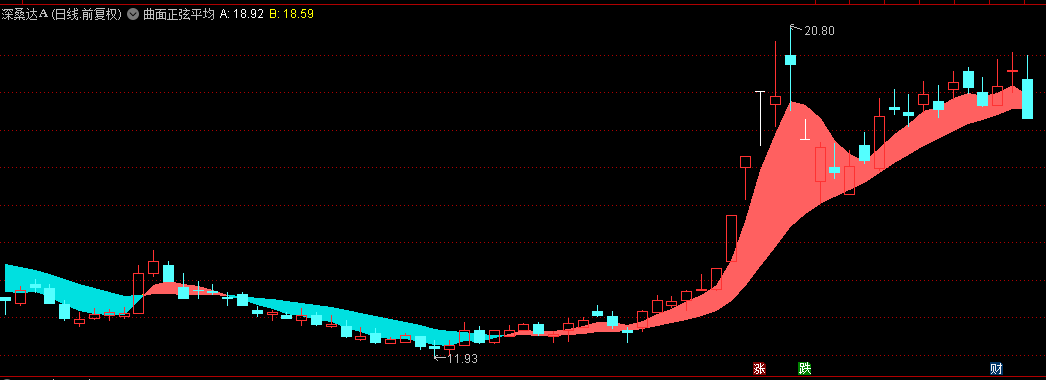
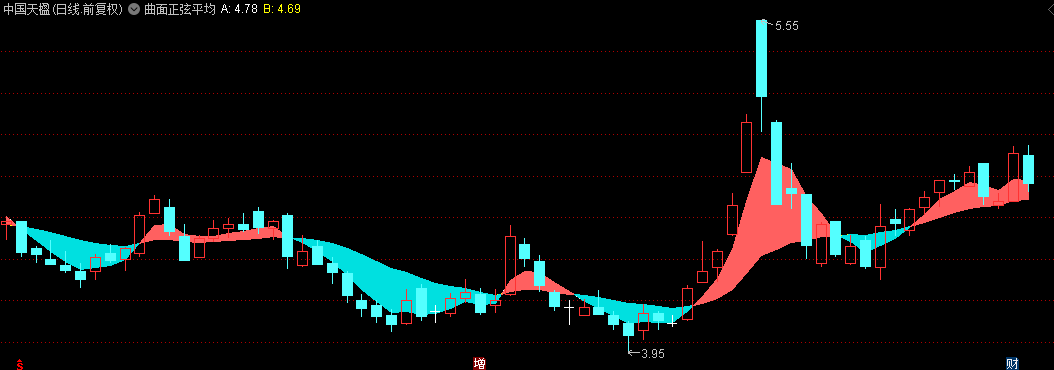
【曲面正弦平均线】主图指标,一种全新的滤波技术,趋势一目了然!
正弦加权移动平均线 (SWMA) 简介
正弦加权移动平均线 (SWMA) 是一种非常有效的平滑时间序列数据的技术。
它是一种加权移动平均线,根据正弦函数为数据点分配不同的权重。
与使用窗口中所有数据点相等权重的传统移动平均线不同,SWMA 为中间数据点分配更高的权重,并为窗口边缘的数据点分配更低的权重。
正弦波是一种平滑、重复的振荡,在 y 的高点和 -y 的低点之间移动。
SWMA 从正弦波周期的前半部分获取权重,因此中间的数据具有最大的权重。
结果与三角移动平均线(TriMA) 非常相似,但计算起来要困难得多。
下面您可以看到如何将权重应用于 50 周期 SWMA、EMA和SMA:
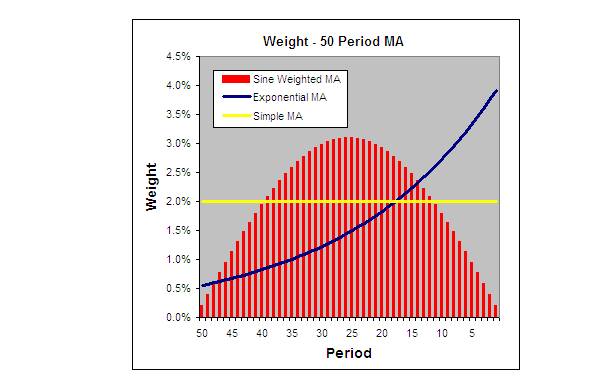
如何计算正弦加权移动平均线
要计算正弦加权移动平均线,请将每个期间的正弦值乘以该期间的收盘价,将结果相加,再将结果除以正弦权重之和。其公式如下:
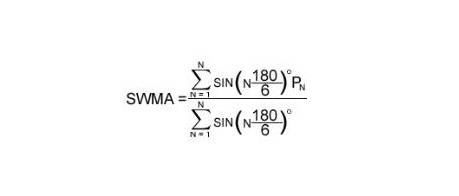
以下是 3 周期正弦加权移动平均线的示例:

数据回测平均胜率与回报率
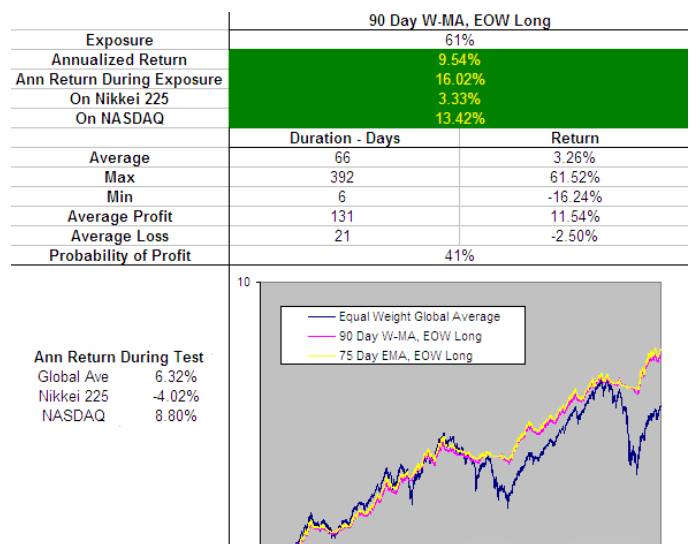
正弦加权移动平均线的优势
有效平滑: SWMA 可以有效地平滑时间序列数据,有效地减少噪声并揭示潜在趋势。通过为更能代表潜在趋势的中心数据点分配更高的权重,SWMA 减少了随机波动和异常值的影响。
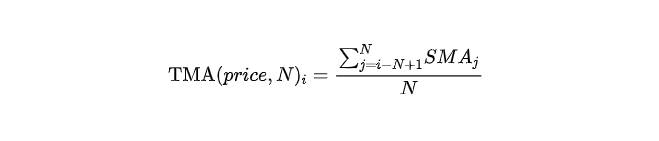
保留重要特征: 与其他一些可能过度平滑数据并掩盖重要特征的平滑技术不同,SWMA 由于其加权方法而保留了关键的数据特征。当处理具有周期性或周期性模式的数据时,此功能尤其有用,因为 SWMA 保持了数据的对称性。
灵活的窗口大小: SWMA 中的窗口大小可以根据数据的特定需求进行调整。较大的窗口大小可以捕捉长期趋势,而较小的窗口大小对于短期模式很有用。这种灵活性允许分析师根据正在分析的时间序列数据的特征来调整平滑过程。
对称权重: 权重的对称分布确保 SWMA 保持数据对称性,使其适用于具有周期性或周期性模式的数据。这种对称性有助于更好地捕捉季节性变化和周期性趋势。
正弦加权移动平均线的实际应用
正弦加权移动平均线在各个领域都有应用:
金融分析: SWMA 可用于平滑股票价格、货币汇率或其他金融指标,以识别长期趋势并减少市场噪音。交易员和分析师经常使用 SWMA 来分析价格走势并预测潜在的市场方向。
气候研究: SWMA 用于分析气候数据,例如温度或降水量,以检测潜在的气候模式和季节性变化。气候科学家使用 SWMA 来深入了解长期气候趋势并识别异常情况。
经济预测: 经济学家使用 SWMA 来预测 GDP、通货膨胀率或失业率等经济指标,从而做出更好的政策决策。准确的经济预测对于政府、企业和投资者有效制定战略至关重要。
信号处理: SWMA 用于信号处理,以消除音频信号、图像处理或通信信号中的噪声。工程师和研究人员使用 SWMA 来提高信号质量并增强各种系统的性能。